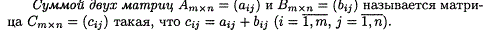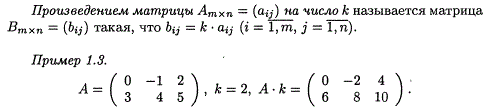Операция сложения матриц вводится только для матриц одинаковых
размеров.
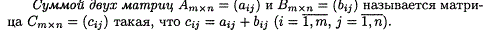
Аналогично определяется разность матриц.
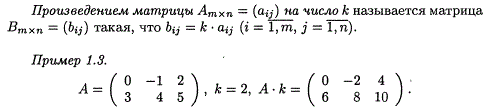
Матрица —А = (—1) • А называется противоположной матрице А.
Разность матриц А — В можно определить так: А — В = А + (—В).
Операции сложения матриц и умножения матрицы на число обладают
следующими свойствами:
1. А+В=В+А
2. А+(В+С)=(А+В)+С;
3. А+О=A;
4. A-A=О;
5. 1*A=А;
6. а•(А+В)=аА+аB;
7. (a+b) • A = аА +bA;
8. а • (bА)=(аb) • А,
Элементарные преобразования матриц
Элементарными преобразованиями матриц являются:
• перестановка местами двух параллельных рядов матрицы;
• умножение всех элементов ряда матрицы на число, отличное от нуля;
• прибавление ко всем элементам ряда матрицы соответствующих
элементов параллельного ряда, умноженных на одно и то же число.
Две матрицы А и В называются эквивалентными, если одна из них
получается из другой с помощью элементарных преобразований.
Записывается А ~ В.
При помощи элементарных преобразований любую матрицу можно
привести к матрице, у которой в начале главной диагонали стоят подряд
несколько единиц, а все остальные элементы равны нулю. Такую матрицу
называют канонической
Операция умножения двух матриц вводится только для случая когда
число столбцов первой матрицы равно числу строк второй матрицы.
Матрицы А и В называются перестановочными, если АВ = В А.
Умножение матриц обладает следующими свойствами:
3. (А + B) • С = АС + ВС;
4. A*(B*C)=(A*B)*C
1. a(A*B)=(aA)*B
2. А • (В + С) = АВ + АС;
Используются технологии
uCoz