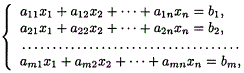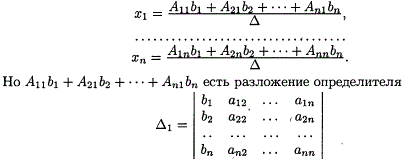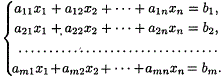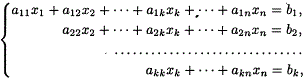Системой линейных алгебраических уравнений, содержащей m
уравнений и n неизвестных, называется система вида
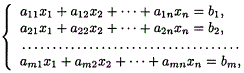
Расширенной матрицей системы называется матрица А системы,
дополненная столбцом свободных членов
Система уравнений называется совместной, если она имеет хотя бы
одно решение, и несовместной, если она не имеет ни одного решения.
Совместная система называется определенной, если она имеет
единственное решение, и неопределенной, если она имеет более одного решения.
В последнем случае каждое ее решение называется частным решением
системы. Совокупность всех частных решений называется общим решением.
Решить систему — это значит выяснить, совместна она или
несовместна. Если система совместна, найти ее общее решение.
Две системы называются эквивалентными (равносильными), если они
имеют одно и то же общее решение. Другими словами, системы
эквивалентны, если каждое решение одной из них является решением другой, и
наоборот.
Эквивалентные системы получаются, в частности, при элементарных
преобразованиях системы при условии, что преобразования выполняются
лишь над строками матрицы.
Система линейных уравнений называется однородной, если все
свободные члены равны нулю:
Теорема
Кронекера-Капелли
Теорема 4.1. Система линейных алгебраических уравнений совместна тогда и
только тогда, когда ранг расширенной матрицы системы равен рангу основной матрицы.
Теорема 4.2. Если ранг совместной системы равен числу неизвестных, то система
имеет единственное решение.
Теорема 4.3. Если ранг совместной системы меньше числа неизвестных, то система
имеет бесчисленное множество решений.

Решение невырожденных линейных систем. Формулы Крамера
Пусть дана система п линейных уравнений с п неизвестными

Отсюда следует, что
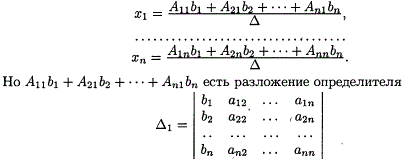
по элементам первого столбца. Определитель Д1 получается из
определителя Д путем замены первого столбца коэффициентов столбцом из
свободных членов.

называются формулами Крамера.
Решение систем линейных уравнений методом Гаусса
Одним из наиболее универсальных и эффективных методов решений
линейных алгебраических систем является метод Гаусса, состоящий в
последовательном исключении неизвестных.
Пусть дана система уравнений
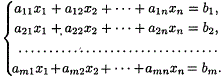
Процесс решения по методу Гаусса состоит из двух этапов. На первом
этапе (прямой ход) система приводится к ступенчатому (в частности,
треугольному) виду.
Приведенная ниже система имеет ступенчатый вид
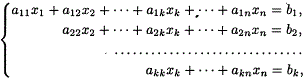
На втором этапе (обратный ход) идет последовательное определение
неизвестных из этой ступенчатой системы.
Используются технологии
uCoz